Teoría De La Computación.: Introducción a la Teoria de Conjuntos

Teoría de Conjuntos:

Historia:

George Cantor (1845-1918) fue quien prácticamente formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas como ya se había hecho con el cálculo cien años antes. Cantor comenzó esta tarea por medio del análisis de las bases de las matemáticas y explicó todo basándose en los conjuntos (por ejemplo, la definición de función se hace estrictamente por medio de conjuntos). Este monumental trabajo logró unificar a las matemáticas y permitió la comprensión de nuevos conceptos.
El problema apareció cuando se comenzaron a encontrar paradojas en esta teoría, siendo la más célebre la paradoja de Russell, y más tarde varios matemáticos encontraron más paradojas, incluyendo al mismo Cantor. Russell descubrió su paradoja en 1901, y la publicó en un apéndice de su libro "Principios de las matemáticas".
Cuando los matemáticos supieron de esta paradoja, muchos se preguntaron si las matemáticas en realidad eran consistentes, y sobre todo verdaderas, ya que cualquier suposición matemática podía basarse en una teoría inconsistente.
La primera propuesta para solucionar el problema de las paradojas provino de un matemático holandés llamado Brouwer, quien propuso una redefinición radical de todas las matemáticas y prometió una solución al conflicto. El programa de Brouwer se basaba en lo más simple de la intuición: el aceptaba los conceptos que son aparentes a la intuición general. Esta filosofía rechazaba muchos principios fundamentales de las matemáticas, pero en cambio, solucionaba satisfactoriamente el problema de las paradojas. Particularmente Brouwer rechazaba el principio del medio excluido, el cuál decía que los elementos de un conjunto o bien tienen una propiedad A o no la tienen, lo cuál sería la negación de la propiedad A. A esta corriente de pensamiento se le llamó intuicionismo.

Por otro lado, David Hilbert se opuso al intuicionismo y aunque no toleraba las paradojas, no estaba dispuesto a ver las matemáticas mutiladas. En 1904 propuso la teoría de la prueba, la cuál era una teoría de la lógica independiente del contexto y podría ser aplicada a las matemáticas sin encontrar paradojas. Russell a su vez desarrolló su teoría de los tipos para evitar las paradojas. El proponía que los enunciados se acomodaran jerárquicamente. Russell publicó sus resultados en 1908 con la colaboración de Alfred North Whitehead.

David Hilbert
La cuarta respuesta a la paradoja fue de Ernst Zermelo en 1908 con la axiomatización de la teoría de conjuntos.
La mejor prueba de que la teoría de conjuntos no ha logrado unificar a las matemáticas es que éstas se han ramificado en áreas muy diferenciadas, como la aritmética, el álgebra, la trigonometría y geometría; también se han separados distintos campos como el cálculo, la topología, la teoría de conjuntos, la teoría de los números y la estadística.

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.
Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas y junto con la lógica permite estudiar los fundamentos de aquélla.
Además, la propia teoría de conjuntos es objeto de estudio no sólo como herramienta auxiliar. En esta disciplina es habitual que se presenten casos de propiedades indemostrables como la hipótesis o la existencia de un cardinal inaccesiblePor esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica.

Definiciones:

Un conjunto es una colección de elementos que se agrupan mediante algunas características en común y que solo aparecen una sola vez.

Otras formas de definir un conjunto son las siguientes:

Es una colección bien definida de objetos o cosas, donde, bien definida significa distinguir con claridad los elementos que forman parte del conjunto.
Son colecciones, agrupaciones o reuniones de elementos a los cuales identificamos por tener propiedades en común.
Es una colección de objetos; en los que a cada uno de los objetos que componen un conjunto se le denomina elemento de un conjunto.

Elemento de un Conjunto:

En teoría de conjuntos, un elemento o miembro de un conjunto (o familia de conjuntos ) es un objeto atómico.

Relación de pertenencia

La relación es un elemento de, también llamada miembro del conjunto, se denota mediante el símbolo e, y al escribir

x e A

estamos diciendo que x es un elemento de A. Equivalentemente, podemos decir o escribir x es un miembro de A, x pertenece a A, x es en A, x reside en A, A incluye x, o A contiene x. La negación de este símbolo se denota .

Relación	Notación	Se lee
pertenencia	$x\in A$	x pertenece a A
inclusión	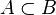$A\subset B$	A está contenido en B
	$A\subseteq B$	A está contenido en B o es igual que B
inclusión	$A\supset B$	A contiene a B
	$A\supseteq B$	A contiene a B o es igual que B

Operaciones entre Conjuntos:

Existen unas operaciones básicas que permiten manipular los conjuntos y sus elementos, similares a las operaciones aritméticas, constituyendo el álgebra de conjuntos:

Unión. La unión de dos conjuntos $A$ y $B$ es el conjunto $A \cup B$ que contiene cada elemento que está por lo menos en uno de ellos.
Intersección. La intersección de dos conjuntos $A$ y $B$ es el conjunto $A \cap B$ que contiene todos los elementos comunes de $A$ y $B$ .
Diferencia. La diferencia entre dos conjuntos $A$ y $B$ es el conjunto $A \ B$ que contiene todos los elementos de $A$ que no pertenecen a $B$ .
Producto cartesiano. El producto cartesiano de dos conjuntos $A$ y $B$ es el conjunto $A \times B$ que contiene todos los pares ordenados $(a, b)$ cuyo primer elemento $a$ pertenece a $A$ y su segundo elemento $b$ pertenece a $B$

Diagramas de Venn:

Con los diagramas de Venn es posible representar las relaciones de intersección, inclusión y disyunción sin cambiar la posición relativa de los conjuntos.

1 Intersección

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.

A = {1; 2; 3; 4; 6; 12} B = {1; 3; 5; 15} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}
A = {x \| x es divisor natural de 12} B = {x \| x es divisor natural de 15} U = {x \| x es natural menor o igual que 16}

2 Inclusión

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo. En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos (regiones vacías), la situación se indica anulándolas (con un color de fondo distinto).

A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
A = {x \| x es divisor natural de 12} B = {x \| x es divisor natural de 6} U = {x \| x es natural menor o igual que 12}

3 Disyunción

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
A = {x \| x es par y de una cifra} B = {x \| x es impar y de una cifra} U = {x \| x es natural menor o igual que 10}

A la izquierda de los diagramas, las definiciones de los conjuntos por enumeración y por comprensión.

Teoría De La Computación.

domingo, 16 de agosto de 2015

Introducción a la Teoria de Conjuntos